Model aggregation: minimizing empirical variance outperforms minimizing empirical error

Context

We present a general framework to combine existing models in a robust manner. Our method is flexible, places few assumptions on the models aggregated, and performs well in our experiments.

See the full article here

Download preprint here

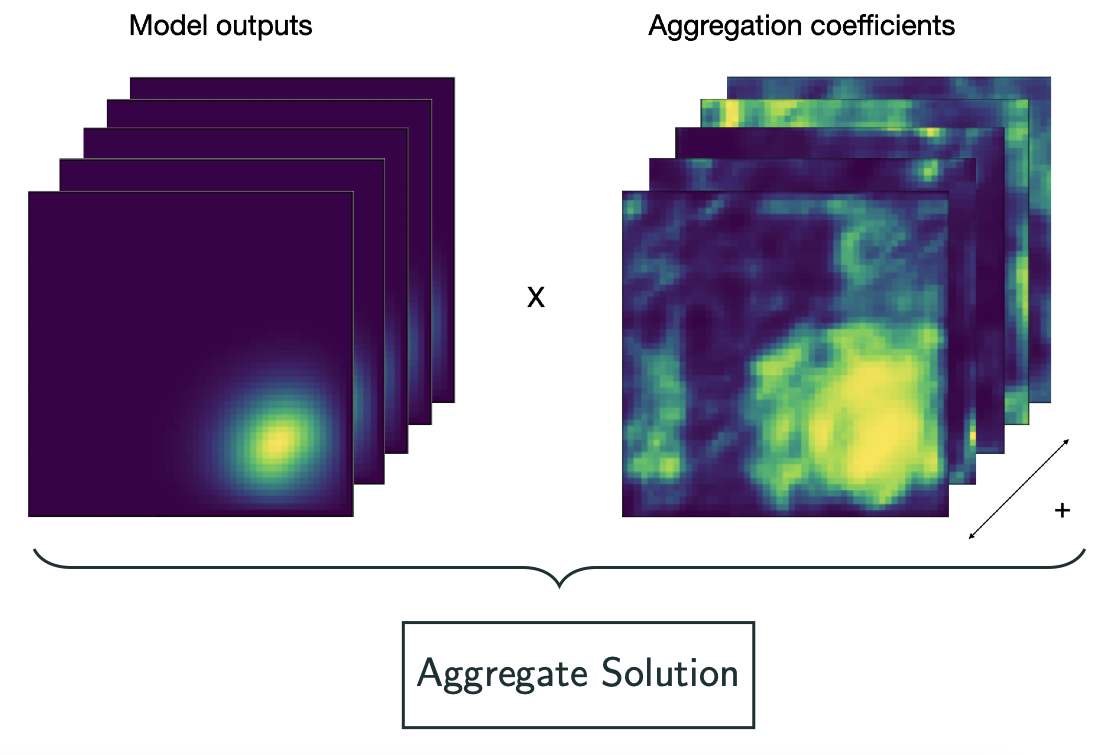
Abstract

Whether deterministic or stochastic, models can be viewed as functions designed to approximate a specific quantity of interest. We propose a data-driven framework that aggregates predictions from diverse models into a single, more accurate output. This aggregation approach exploits each model’s strengths to enhance overall accuracy. It is non-intrusive - treating models as black-box functions - model-agnostic, requires minimal assumptions, and can combine outputs from a wide range of models, including those from machine learning and numerical solvers. We argue that the aggregation process should be point-wise linear and propose two methods to find an optimal aggregate: Minimal Error Aggregation (MEA), which minimizes the aggregate’s prediction error, and Minimal Variance Aggregation (MVA), which minimizes its variance. While MEA is inherently more accurate when correlations between models and the target quantity are perfectly known, Minimal Empirical Variance Aggregation (MEVA), an empirical version of MVA - consistently outperforms Minimal Empirical Error Aggregation (MEEA), the empirical counterpart of MEA, when these correlations must be estimated from data. The key difference is that MEVA constructs an aggregate by estimating model errors, while MEEA treats the models as features for direct interpolation of the quantity of interest. This makes MEEA more susceptible to overfitting and poor generalization, where the aggregate may underperform individual models during testing. We demonstrate the versatility and effectiveness of our framework in various applications, such as data science and partial differential equations, showing how it successfully integrates traditional solvers with machine learning models to improve both robustness and accuracy.